5. Cross Product

d. 1. Volume

Parallelepiped

Consider a parallelepiped where the base has adjacent edges \(\vec u\), \(\vec v\) and \(\vec w\). Take \(\vec u\) and \(\vec v\) as the edges of the base. Let \(\theta\) be the angle between \(\vec u\) and \(\vec v\) and let \(\phi\) be the angle between \(\vec w\) and the perpendicular to the base which is \(\vec u\times\vec v\).

The volume of the parallelepiped is the product of the area of the base and its height \[ V=BH \] The area of the base parallelogram is \(B=|\vec u\times\vec v|\) and the height is \(H=|\vec w|\cos\phi\) (assuming \(\phi\) is acute, as in the first figure). Thus:

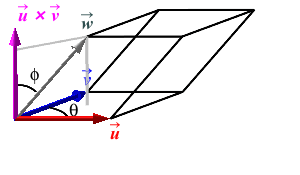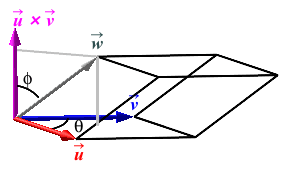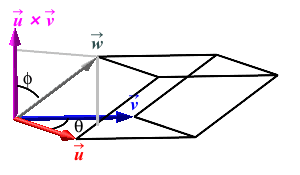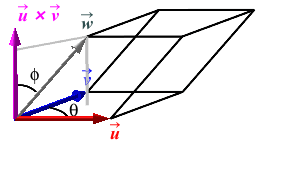
DefVolParaUp

\[ V=BH =|\vec u\times\vec v|\,|\vec w|\cos\phi \] However, this is just the dot product of \(\vec u\times\vec v\) and \(\vec w\). Therefore, \[ V=\vec u\times\vec v\cdot\vec w \] There is one technicality here. We need the volume to be positive, but the triple product could be negative. In the figure above, we chose \(\vec u\) and \(\vec v\) so that \(\vec u\times\vec v\) points to the same side as \(\vec w\). So \(\phi \lt 90^\circ\) and \(\cos\phi \gt 0\). However, if we interchange the names \(\vec u\) and \(\vec v\), (as in the figure at the right) then \(\vec u\times\vec v\) points to the opposite side as \(\vec w\) as in the figure. So \(\phi \gt 90^\circ\) and \(\cos\phi \lt 0\). So we need to use \(|\cos\phi|\) to compute the height \(H=|\vec w|\,|\cos\phi|\). So the volume is \(V=|\vec u\times\vec v|\, |\vec w|\,|\cos\phi| =|\vec u\times\vec v\cdot\vec w|\), the absolute value of the triple product.

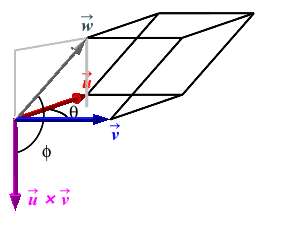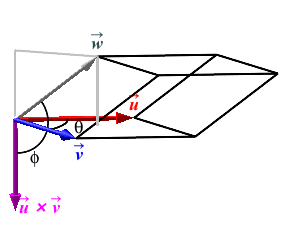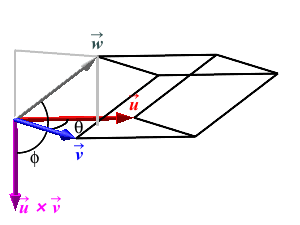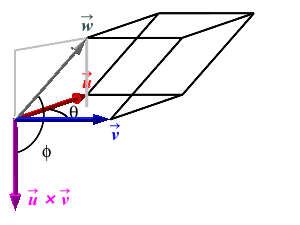
DefVolParaDn

The Volume of a Parallelepiped with adjacent edges \(\vec u\), \(\vec v\) and \(\vec w\) is: \[ V=|\vec u\times\vec v\cdot\vec w| \]

Notice that the volume is just the absolute value of the triple product. This is fortunate because there is no reason that we need to take \(\vec u\) and \(\vec v\) to be the edges of the base. So the formula for the volume could have \(\vec u\), \(\vec v\) and \(\vec w\) in any order. Luckily, the triple product is the same in any order up to a minus sign and the absolute value cancels off this minus. So the volume is the absolute value of the triple product in any order.

Find the volume of the parallelepiped with adjacent edges \(\overrightarrow{AB}\), \(\overrightarrow{AC}\) and \(\overrightarrow{AD}\) where: \[ A=\left\langle 3,1,0\right\rangle, B=\left\langle 3,0,2\right\rangle, C=\left\langle 2,3,0\right\rangle \text{ and } D=\left\langle 4,1,3\right\rangle \]

The adjacent edges are \[\begin{aligned} \overrightarrow{AB}&=B-A =\left\langle 3,0,2\right\rangle-\left\langle 3,1,0\right\rangle =\left\langle 0,-1,2\right\rangle \\ \overrightarrow{AC}&=C-A =\left\langle 2,3,0\right\rangle-\left\langle 3,1,0\right\rangle =\left\langle -1,2,0\right\rangle \\ \overrightarrow{AD}&=D-A =\left\langle 4,1,3\right\rangle-\left\langle 3,1,0\right\rangle =\left\langle 1,0,3\right\rangle \end{aligned}\] Their triple product is \[ \overrightarrow{AB}\times\overrightarrow{AC}\cdot\overrightarrow{AD} =\begin{vmatrix} 0 & -1 & 2 \\ -1 & 2 & 0 \\ 1 & 0 & 3 \end{vmatrix} =-7 \] So the volume is \[ V =\left|\overrightarrow{AB}\times\overrightarrow{AC}\cdot\overrightarrow{AD}\right| =7 \]

Find the volume of the parallelepiped with adjacent edges \(\vec u=\left\langle 2,3,1\right\rangle\), \(\vec v=\left\langle 2,0,-1\right\rangle\) and \(\vec w=\left\langle 0,-2,3\right\rangle\).

\(V=26\)

The triple product is \[ \vec u\times\vec v\cdot\vec w =\begin{vmatrix} 2 & 3 & 1 \\ 2 & 0 & -1 \\ 0 & -2 & 3 \end{vmatrix} =-26 \] So the volume is \[V=|\vec u\times\vec v\cdot\vec w|=26\]

© MYMathApps

Supported in part by NSF Grant #1123255